How to solve a sliding puzzle

When I was 13, I got a 3x3 sliding tile puzzle. Back then, I went to a boarding school with no internet nor TV. It was 1999 in Thailand; the internet wasn't prevalent yet anyway. I had a lot of time in my hand and channeled the free time to find an intuitive way to solve this puzzle.

Just like every difficult puzzle, the sliding tile puzzle is designed to have "local maximas" where you will never solve it if you simply try to arrange all the pieces into their final places. You will be stuck in a local maxima.

For the sliding tile puzzle, my aha moment was that the correct subproblem to solve is the relative positions between each piece. Once the relative positions of every piece are correct, we can make the final moves to get every piece into its final place. Every piece (or most pieces) has to move into its final position at the same time.

The relative positions to maintain is on the border where 2 should follow 1, 3 should follow 2, 4 should follow 3, and so on ... around the border.

For example, if 1 is at the top left position, then we should move 2 to the middle right position. If we "rotate" the border 3 times counter-clockwise where 1 arrives at the top left position (which is its final position), 2 will naturally be at the top middle position (which is also its final position).

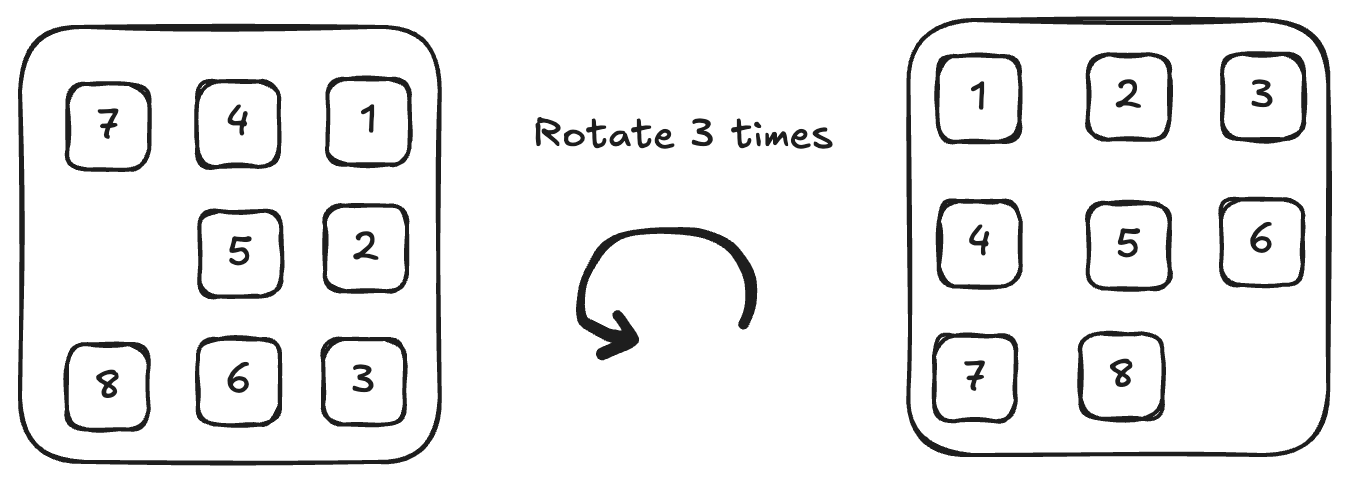
We, then, utilise the centre position as the buffer space in order to rearrange the order of the pieces on the border. For example:

Now 2 is in the correct position relative to 1.

Once the order of the pieces on the border is correct, we simply "rotate" the border until every number is in its final position.

This intuitive way of thinking about the sliding tile puzzle works with any size of the sliding tile puzzle.

One note is that this strategy doesn't find the fewest number of moves to solve the puzzle. That can only be achieved by the breadth first search algorithm and maybe A*(?).

I hypothesize that we can solve a rubik using the same strategy because we can also be stuck in local maximas i.e. most pieces would have to move into its final position all at once. I'll report back whether this strategy of "relative positions" will work or not.